TIPOS DE FUNCIONES

TIPOS DE FUNCIONES

Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera corresponde un único valor de la segunda.

Leer más: http://www.monografias.com/trabajos100/matematicas-funciones-y-tipos-funciones/matematicas-funciones-y-tipos-funciones.shtml#ixzz384Z2jmbN

De acuerdo a ciertas características las funciones se clasifican:

1. FUNCIONES ALGEBRAICAS

En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radiación.

Las funciones algebraicas pueden ser:

Funciones explícitas

Si se pueden obtener las imágenes de x por simple sustitución.

f(x) = 5x − 2

Funciones implícitas

Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.

5x − y − 2 = 0

1.1. FUNCIONES POLINÓMICAS

Son las funciones que vienen definidas por un polinomio.

f(x) = a₀ + a₁x + a₂x² + a₂x³ +··· + a_nxⁿ

Su dominio es , es decir, cualquier número real tiene imagen.

1.1.1.FUNCIONES CONSTANTES

f (x) = k

Donde x es igual a un número real y el rango es un único valor.

Siempre va hacer una linea horizontal, con angulo (0) y pendiente (0), va del menos al mas infinito.

1.1.2 FUNCIONES POLINÓMICA DE PRIMER GRADO

f(x) = mx + n

Su gráfica es una recta oblicua, que queda definida por dos  puntos de la función.

Son funciones de este tipo las siguientes:

• Función afín
• Función lineal
• Función identidad

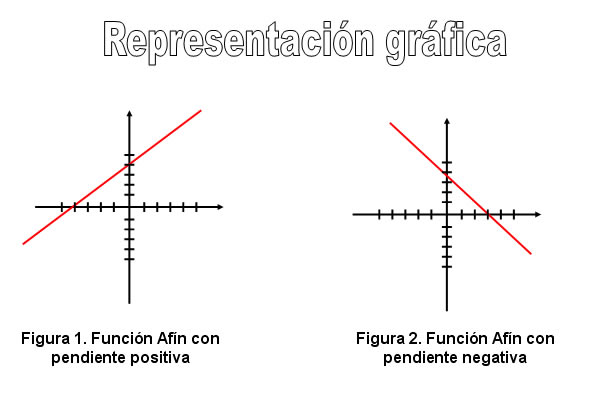
1.1.2.1. FUNCIÓN AFÍN

y = mx + n

m es la pendientee de la recta (grado de inclinación). Si m es positiva la recta es creciente y si es negativa decreciente.

1.2.1.2.FUNCIÓN LINEAL

y = mx

m es la pendiente de la recta (grado de inclinación)

Es continua

Es una linea recta

Puede ser creciente o decreciente

Tiene pendiente positiva o negativa

Es de primer grado

1.2.1.3. FUNCIÓN IDENTIDAD

f(x) = x

Su gráfica es la directriz del primer grado y tercer cuadrante

Función continua

Dominio del (-) infinito hasta mas infinito

Es de primer grado (Linea Recta)

Tiene pendiente (creciente)

Su angulo de inclinación es de 45 grados

Pasa por el origen

1.1.3. FUNCIONES CUADRÁTICAS

f (x) = ax² + bx + c

Son funciones polinómicas de segundo grado

Su gráfica es una parábola

1.2. FUNCIONES RACIONALES

 

Sus gráficas son hipérbolas, dos gráficas en cuadrantes cruzados

Son fraccionarios

Donde a (x) y b(x) son funciones polinómicas

El dominio consiste de todos los valores de x tal que a(x) ≠ 0

Tiene ASINTOTA, es una recta a la cual se aproxima la gráfica, al crecer indefinidamente "x" o "y", pero nunca la toca

Tiene un HUECO, representa el valor que no se le puede asignar a la función por presentar una indeterminación al sustituir la variable "x" en la misma.

CARACTERÍSTICAS

·       Su dominio excluye a los valores de ¨x¨ que hacen cero su denominador.

·        Es discontinua de forma general pero continua en determinadas intervalos.

·        Puede tener o no raíces

·        Grado variable

·        Tiene asintontas vertical, horizontal u oblicua.

·        Su gráfica es una Hipérbola

Si ¨n¨ es impar entonces la grafica es como se muestra.

Si ¨n¨ es par entonces la gráfica es como se muestra.

1.3. FUNCIONES RADICALES

f(x) = √x

Una función radical es una función cuya regla es una expresión radical

Una función raíz cuadrada es una función radical que envuelve √x

Función radical de índice impar

El dominio es .

Función radical de índice par

El dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.

1.4. FUNCIONES ALGEBRAICAS A TROZOS

Son funciones definidas por distintos criterios, según los intervalos que se consideren

También denominadas función por partes, función seccionada o función definida por tramos.

Es una función cuya definición (la regla que define la dependiente), llamada regla de correspondencia

Cambia dependiendo de el valor de la variable independiente.

Son funciones de este tipo las siguientes:

• Función parte entera de x
• Función Mantisa
• Función de Signo
• Función valor absoluto

1.4.1. FUNCIÓN PARTE ENTERA DE X

f(x) 0 E(x)

Es una función que a cada número real hace corresponder el número entero inmediatamente inferior.

1.4.2. FUNCIÓN MANTISA

f(x) = x - E(x)

Función que hace correspondencia a cada número el mismo número menor su parte entera.

1.4.3. FUNCIÓN SIGNOS

f(x) = sgn(x)

1.4.4. FUNCIÓN VALOR ABSOLUTO

f(x) = lxl

Es termino surge de nociones geométricas, y se relaciona con los concepto de longitud y distancia.

La función en valor absoluto siempre representan una distancia o intervalos (tramos o trozos), y se pueden resolver o calcular

D =

2. FUNCIONES TRASCENDENTES

La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

2.1. FUNCIÓN EXPONENCIAL

El dominio de la función f es el conjunto de todos los números reales.

El rango de f es el intervalo (0, + infinito)

La gráfica de f tiene una asíntota horizontal dad por y=0

Función f tiene interceptar a y en (0,1), f es una función creciente si a es mayor que 1 y una función decreciente si a es menor que 1.

2.2. FUNCIÓN LOGARÍTMICA

Dominio: 

Recorrido: 

Es continua.

Los puntos (1, 0) y (a, 1) pertenecen a la gráfica.

Es inyectiva (ninguna imagen tiene más de un original).

Creciente si a>1.

Decreciente si a<1.

Las gráfica de la función logarítmica es simétrica (respecto a la bisectriz del 1^er y 3^ercuadrante) de la gráfica de la función exponencial, ya que son funciones reciprocas o inversas entre sí.

2.3. FUNCIÓN TRIGONOMÉTRICAS

Las funciones trigonométricas son funciones de un ángulo (seno, coseno y tangente); tienen importancia en el estudio de la geometría de los triángulos y en la representación de fenómenos periódicos.

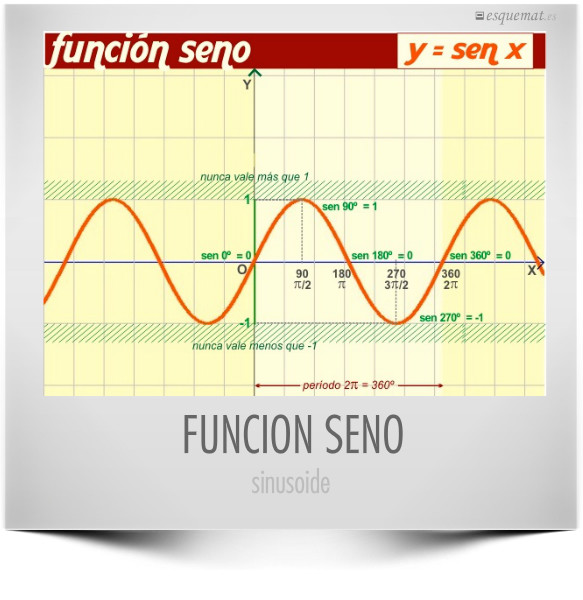
2.3.1. FUNCIÓN SENO

Dominio: 

Recorrido: [−1, 1]

Período: 

Continuidad: Continua en 

Impar: sen(−x) = −sen x

La función y=sen x es impar, ya que sen(-x)=senx, para todo x en 

El valor máximo de senx es 1, y el mínimo valor es -1.

2.3.2. FUNCIÓN COSENO

Dominio: 

Recorrido: [−1, 1]

Período: 

Continuidad: Continua en 

Par: cos(−x) = cos x

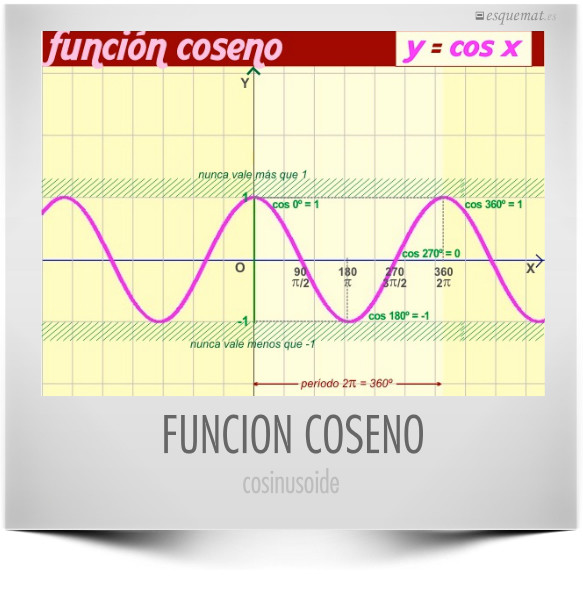
La gráfica ilustra los valores máximo(1) y mínimo (-1) que alcanza el coseno y el período de 360º

2.3.3. FUNCIÓN TANGENTE

Dominio: 

Recorrido: 

Continuidad: Continua en 

Período: 

Impar: tg(−x) = −tg x

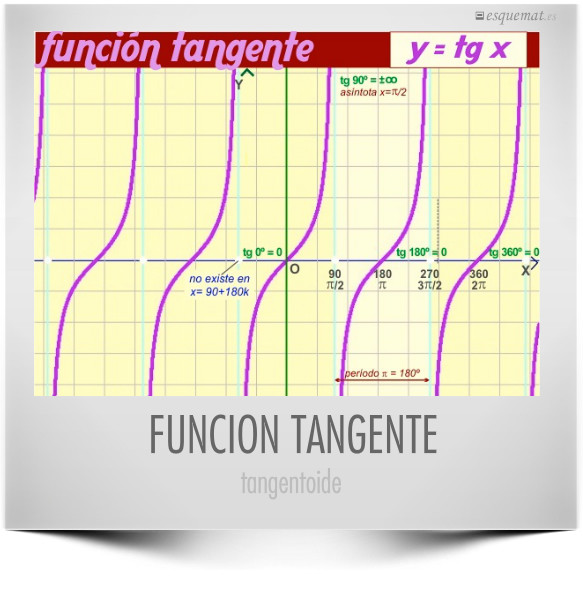
La gráfica ilustra los puntos de discontinuidad (míltiplos impares de 90º) y las tendencias al infinito, con sus asíntotas.

2.3.1. FUNCIÓN COTANGENTE

Dominio:

Recorrido: 

Continuidad: Continua en 

Período: 

Impar: cotg(−x) = −cotg x

2.3.1. FUNCIÓN SECANTE

Dominio: 

Recorrido: (− ∞, −1]  [1, ∞)

Período: 

Continuidad: Continua en 

Par: sec(−x) = sec x

2.3.1. FUNCIÓN COSECANTE

Dominio: 

Recorrido: (− ∞, −1]  [1, ∞)

Período: 

Continuidad: Continua en 

Impar: cosec(−x) = −cosec x

Transformaciones de la Función

Las transformaciones, desplazamientos o traslaciones son transformaciones que cambian la posición de la gráfica de una función. La forma general de la grafica de una función se traslada hacia arriba, abajo, a la derecha o a la izquierda. Las traslaciones son consideradas transformaciones rígidas.

USO DE FUNCIONES EN LA VIDA COTIDIANA

FUNCIÓN	EJEMPLO USO
Lineal	La función que representa el espacio recorrido por un móvil, con velocidad uniforme que parte del reposo e(t)=vt que es una función del tipo f(x)=mx cuya gráfica es una recta dependiente de m y que pasa por el origen de coordenadas.
Afin	Si un consumidor desea adquirir cualquier producto, este depende del precio en que el artículo esté disponible. Una relación que especifique la cantidad de un artículo determinado que los consumidores estén dispuestos a comprar, a varios niveles de precios, se denomina ley de demanda. La ley más simple es una relación del tipo P= mx + b, donde P es el precio por unidad del artículo y m y b son constantes.
Cuadrática	En el lanzamiento de proyectiles y=ax2+bx+c Ejemplo: Si queremos calcular la distancia que alcanza un objeto que es lanzado hacia arriba con una inclinación determinada α y a una velocidad inicial de lanzamiento V° en función del tiempo se puede representar de forma gráfica y algebraica.
Racionales	·         Isaac Newton enunció que la fuerza con que se atraen dos cuerpos es directamente proporcional al producto de sus masa e inversamente proporción al cuadrado de la distancia que le separa, se expresa matemáticamente como : F=G Mm/d2          ·         La ley de Coulomb nos dice que la fuerza de atracción o de repulsión de dos cargas es directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado de la distancia que las separa, se expresa matemáticamente como F= K Qq/d2
Radical	Cuando se quiere calcular el ángulo de un péndulo T, que está en función de la longitud del péndulo de la forma: T=2√I
Logarítmicas	·         La ley de medida de la intensidad de una onda que viene dada por b=10.log I/Io siendo I la intensidad física del sonido, Io la intensidad de referencia.          ·         La escala de Richter M=Log 10 P donde M es la magnitud del terremoto, P indica el número de veces que ha sido mayor la amplitud de la onda sísmica producida por el terremoto, en comparación con la onda en una situación sin terremoto.
Exponenciales	·         Con el descubrimiento del Polonio (elemento radioactivo) descubierto por Marie Curie en 1 898 decae exponencialmente de acuerdo a la función: m = m0 e-0,005t, donde m0 es la masa inicial del Polonio, m es la masa al cabo de un tiempo y t es el tiempo en días          ·         El crecimiento poblacional ( Demografía) de una región o población en años, parece estar sobre una curva de característica exponencial que sugiere el modelo matemático dado por: N = N0 ekt, donde N0 es la población inicial, t es el tiempo transcurrido en años y k es una constante.
Trigonométricas	Las funciones trigonométricas son funciones de un ángulo (seno, coseno y tangente); tienen importancia en el estudio de la geometría de los triángulos y en la representación de fenómenos periódicos. Son utilizadas frecuentemente en cálculos técnicos, para topografías la tierra los topógrafos la dividen en triángulos y marcan cada ángulo con un "punto de referencia”. Un gran proyecto de reconocimiento de los 1800s fue la "Gran Planimetría Trigonométrica" de la India británica. Hoy en día la posición sobre la Tierra se puede localizar de forma muy precisa usando el sistema de posicionamiento global (GPS) de 24 satélites en órbita exacta, que están difundiendo constantemente su posición. Un pequeño instrumento electrónico de mano recibe sus señales y nos devuelve nuestra posición con un error de 10-20 metros ( aún es más preciso para usos militares, los patrocinadores del sistema). Se usa una gran cantidad de trigonometría, pero lo hace todo la computadora que está dentro de su aparato, lo único que usted necesita es pulsar los botones apropiados. -        .